
En el recién despedido año 2022, Netflix lanzó la serie Los Apocalipsis del Pasado, conducida por el escritor británico Graham Hancock. La serie de televisión muestra en sus primeros dos episodios unas construcciones arquitectónicas erigidas por civilizaciones ancestrales, hoy extintas.
El segundo episodio de la serie, Hancock presenta la gran pirámide de Cholula, y culmina con la pirámide de Gunung Padang, entre otras.
Si bien las construcciones que Hancock nos presenta en su serie son imponentes; y de una gran riqueza arquitectónica, arqueológica y antropológica,hay una imprecisión conceptual al llamar pirámides a estas estructuras. Invito cordialmente al lector a seguirme en las próximas líneas, para que pueda comprender lo que trato de decir. Si tú, querido lector, no estás familiarizado con las matemáticas, te invito cordialmente a omitir los detalles de los cálculos, e ir directo a las conclusiones, al final de la entrega.
Comencemos con la definición de pirámide. Una pirámide es un poliedro generado por un polígono base y un vértice, fuera del plano del polígono, al que llamamos ápice. Si unimos cada vértice del polígono base con el ápice creamos una arista de la pirámide. Cada lado del polígono base es una arista de la pirámide. La porción del plano que generan dos vértices consecutivos del polígono base con el ápice es una cara de la pirámide. El polígono base es una cara de la pirámide.
Por lo tanto, podemos describir por completo una pirámide en términos de sus vértices (los del polígono base y el ápice), sus aristas y sus caras. Veamos algunos ejemplos: el tetraedro es una pirámide de base triangular.
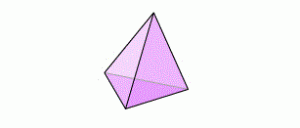
Figura 1. Pirámide de base triangular
Si representamos por V al número de vértices, por A al número de aristas y por C al número de caras, tenemos en el caso del tetraedro que V = 4, A = 6, C = 4. Un simple cálculo muestra que V – A + C = 2. Sigamos, la pirámide de base cuadrada se ilustra a continuación:
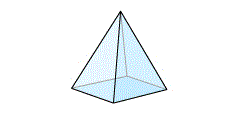
Figura 2. Pirámide de base cuadrada
Aquí, V = 5, A = 8, C = 5. Una vez más, V – A + C = 2. ¿Coincidencia? Veamos un último ejemplo, en la pirámide de base pentagonal.
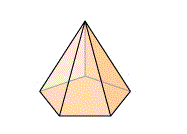
Figura 3. Pirámide de base pentagonal
Nuevamente, V = 6, A = 10, C = 6 y por tanto V – A + C = 2. Llamemos χ = V – A + C. Al número χ se le conoce como la característica de Euler o simplemente característica. Leonhard Euler fue un célebre matemático suizo quien demostró que en todo poliedro cerrado y convexo se cumple que χ = 2.
Haz el esfuerzo, querido lector. Si en general tenemos una pirámide con base el polígono regular de n lados, tenemos que V = n + 1, A = 2n, C = n + 1 y por tanto χ = 2.
La característica de Euler es una propiedad invariante de los poliedros cerrados y convexos. Hay una rama de la matemática que se llama topología que se encarga del estudio de dichos invariantes.
Pero aún más, en el caso de las pirámides truncadas (aquellas en las que removemos una porción de la pirámide que contiene el ápice) también χ = 2. Voy a ilustrar solamente el caso de la pirámide de base cuadrada truncada.
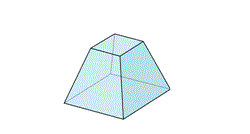
Figura 4. La pirámide de base cuadrada truncada
Aquí, V = 8, A = 12, C = 6, entonces χ = 2. En general para la pirámide truncada de base poligonal de n lados, se tiene que V = 2n, A = 3n, C = n + 2, por lo cual χ = 2.
Ahora, voy a hablar un poco de la convexidad. Una figura convexa es aquella que mantiene en su interior cualquier segmento de recta que une dos puntos internos de la figura, de lo contrario es cóncava. En la ilustración la figura verde es convexa, en donde todos sus ángulos internos son agudos.Mientras que en la figura morada es cóncava, ya que uno de los ángulos internos es obtuso.
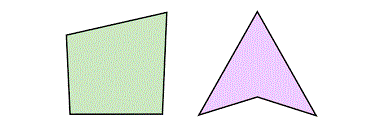
Figura 5. Convexo (izquierda) y cóncavo (derecha)
En síntesis, una pirámide, completa o truncada es un poliedro convexo con χ = 2.
Una vez aclaradas la convexidad y la característica de Euler, volvamos a las estructuras que Hancock nos presenta.La gran pirámide de Cholula se muestra a continuación

Figura 6. La gran pirámide de Cholula (extracto)
Esta construcción arquitectónica es una estructura piramidal escalonada, nótese que uso la frase sustantivada estructura piramidal escalonada en lugar del sustantivo pirámide, debido a lo siguiente. La gran pirámide de Cholula es cóncava. Tómese dos puntos cualesquiera entre un escalón y otro, es evidente que hay porciones del segmento de recta fuera de la estructura piramidal, por lo tanto, se pierde la convexidad.
Pero también se pierde la característica de Euler: cada terraza tiene forma de pirámide truncada, pero al colocar una terraza sobre otra se sobreponen dos caras de cada pirámide truncada, resultando en un cuadrado la intersección de ambas caras.
El cuadrado tiene característica 1, ya que V = 4, A = 4, C = 1, entonces χ = 1. Por lo tanto, la característica de dos terrazas consecutivas es la suma de sus características menos la característica de un cuadrado, es decir χ = 2 + 2 – 1 = 3. Repitiendo el proceso hasta la última terraza, concluimos que la característica de la gran pirámide de Cholula es χ = 3.
Al ser una estructura piramidal cóncava con característica de Euler χ = 3 . La gran pirámide de Cholula no es una pirámide.
El resto de las estructuras arquitectónicas que Hancock presenta en su serie de Netflix, tampoco son pirámides. Son estructuras piramidales escalonadas.

Figura 7. La pirámide de Gunung Pandang
Por economía de lenguaje, conviene llamar pirámides a estas estructuras piramidales escalonadas. No tengo ningún problema con eso. Me parece apropiado aclarar el punto desde la rigurosidad de la geometría clásica griega y la belleza de la topología que, entre otros, dio sus primeros pasos con Euler.
Hasta una próxima entrega.
© Imágenes tomadas de MathMonks y Google Imágenes
Acerca del autor. Tomás Guardia es doctor en matemáticas egresado de la Universidad Central de Venezuela. Actualmente, es profesor de la Universidad de Gonzaga y de la Universidad de Stanford en Estados Unidos. Con más de años de experiencia docente a nivel universitario, una de sus pasiones es la divulgación y la enseñanza de la matemática.
Noticias Relacionadas
El periodismo independiente necesita del apoyo de sus lectores para continuar y garantizar que las noticias incómodas que no quieren que leas, sigan estando a tu alcance. ¡Hoy, con tu apoyo, seguiremos trabajando arduamente por un periodismo libre de censuras!
Apoya a El Nacional













