La paradoja de la suma

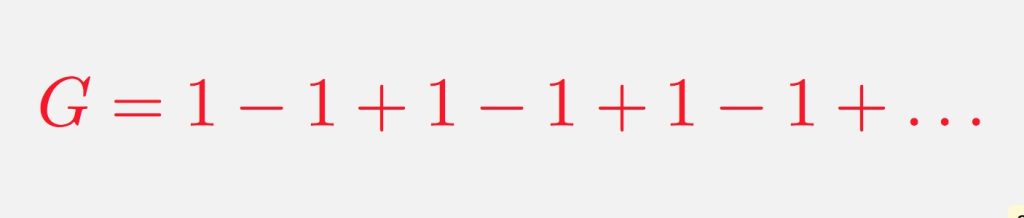
Este artículo es una traducción libre -y resumida- de otro publicado en el portal de Scientific American por Jack Murtagh y que ustedes pueden ubicar aquí.

I

¿Cuánto es uno menos uno? Cero. Hasta aquí, todo bien. Si luego sumamos un 1, la suma crece, pero si restamos otro uno, volvemos a cero. Digamos que seguimos -a lo Ilan Chester- haciendo esto para siempre:

1 – 1 + 1 – 1 + 1 – 1 +…

¿Cuál es la suma resultante? La pregunta parece simple, incluso tonta, pero desconcertó a algunos de los matemáticos más grandes del siglo XVIII. 

La paradoja es la esencia del problema porque múltiples argumentos aparentemente sólidos sobre “la suma” alcanzan conclusiones radicalmente diferentes. La primera persona en investigar profundamente este problema pensó que dicho problema explicaba cómo Dios creó el universo. En términos modernos ilustra que las matemáticas son un esfuerzo más humano de lo que a veces se aprecia.

Haga el lector un ejercicio sobre lo que, en su opinión, es el resultado de la suma de la serie infinita. A fin de ayudarlo, se suministran varias alternativas de respuesta: a) 0; b) 1; c) ½ ; y d) El resultado es nada, es decir, no hay resultado.

El argumento para la alternativa a) (cero) surge de manera natural al incluir paréntesis sugerentes:

(1 – 1) + (1 – 1) + (1 – 1) +…

Recuerden que, en matemáticas, el orden de las operaciones dicta que primero evaluemos las que están dentro de los paréntesis antes de evaluar las que están fuera. Cada (1 – 1) se cancela a 0, por lo que lo anterior resulta en 0 + 0 + 0 +… lo que, claramente, equivale a cero.

Ahora bien y dado que la serie es infinita, un pequeño cambio en los paréntesis produce un resultado diferente. En lugar de emparejar los dos primeros términos y los dos siguientes, y así sucesivamente, si dejamos de lado el primer 1, entonces el segundo y el tercer término también se cancelan, y el cuarto y el quinto se cancelan y así sucesivamente:

1 + (–1 + 1) + (–1 + 1) + (–1 + 1) +…

Nuevamente, todos los paréntesis suman 0, pero tenemos este 1 positivo extra al principio, lo que sugiere que toda la expresión suma 1.

El monje italiano y matemático Luigi Guido Grandi (1671-1742) investigó por primera vez la serie, definida como la suma de un número infinito de términos, en 1703. Grandi, a quien se le atribuye el nombre de la serie de marras, observó que al simplemente cambiar los paréntesis podía hacer que la serie sumara 0 ó 1. Según el historiador italiano de matemáticas Giorgio Bagni (1958-2009), esta inconsistencia aritmética tenía un significado teológico para Grandi, quien creía que mostraba que la creación de la nada era “perfectamente plausible”.

II

La paradoja de la serie de Grandi se enmarca en un contexto más amplio de series infinitas que han desconcertado a los pensadores desde la antigüedad, como las paradojas de movimiento de Zenón de Elea (490 a.C–430 a.C). La resolución de estas paradojas y el entendimiento de series infinitas avanzaron significativamente con el desarrollo del cálculo a finales del siglo XIX.

Los matemáticos modernos utilizan el concepto de convergencia para resolver estas paradojas. Si las sumas parciales de una serie infinita tienden hacia un valor fijo, se dice que la serie converge a ese valor. Sin embargo, las sumas parciales de la serie de Grandi oscilan entre 0 y 1 sin acercarse a un valor único, lo que sugiere que la serie no converge.

Existen otros métodos para sumar series infinitas que pueden asignar valores diferentes a una misma serie. Un ejemplo es la suma de Cesàro (Ernesto Cesàro, matemático italiano que vivió entre 1859 y 1906), que toma el promedio de las sumas parciales sucesivas. Curiosamente, la serie de Grandi tiene una suma de Cesàro de ½, lo que refuerza la respuesta defendida por Grandi y Leibniz.

Gottfried Wilhelm Leibniz (1646-1716) estuvo de acuerdo con la conclusión de Grandi, pero trató de respaldarla con razonamientos probabilísticos. Leibniz argumentó que si detienes la suma de la serie infinita de términos en un punto elegido al azar, entonces la suma hasta ese punto será 0 ó 1 con igual probabilidad, por lo que tiene sentido promediarlos a ½. Es decir, dado que las dos series resultantes de términos son infinitas, tiene sentido utilizar el promedio de los valores esperados. Leibniz pensó que el resultado era correcto, pero reconoció que su argumento era más “metafísico que matemático”. 

III

El artículo de Jack Murtagh concluye que, aunque la definición de convergencia basada en sumas parciales es la más aceptada, existen otras formas de abordar la suma de series infinitas que son útiles en ciertos contextos. En el caso de la serie de Grandi, la respuesta podría ser la d) el resultado es nada, pero si tuviera que haber un resultado, sería la c) ½. Esto conduce a una conjetura sobre las matemáticas: a pesar de su percibida objetividad, son un esfuerzo humano influenciado por convenciones e, incluso, decisiones colectivas.